Combining satellite data with tidal modelling 
Sign up to the DEA Sandbox to run this notebook interactively from a browser
Compatibility: Notebook currently compatible with the
DEA Sandboxenvironment onlyProducts used: ga_ls8c_ard_3
Background
Ocean tides are the periodic rise and fall of the ocean caused by the gravitational pull of the moon and sun and the earth’s rotation. Tides in coastal areas can greatly influence how these environments appear in satellite imagery as water levels vary by up to 12 metres (e.g. in north-western Australia). To be able to study coastal environments and processes along Australia’s coastline, it is vital to obtain data on tidal conditions at the exact moment each satellite image was acquired.
Description
This notebook demonstrates how to combine remotely sensed imagery with information about ocean tides using functions from the `dea_tools.coastal module <../Tools/dea_tools/coastal.py>`__, allowing us to analyse satellite imagery by tidal stage (e.g. low, high, ebb, flow). These functions use the Finite Element Solution 2014 (FES2014) tidal model to calculate the height (relative to mean sea level, i.e. approximately equivalent to the
Australian Height Datum or AHD) and stage of the tide at the exact moment each satellite image was acquired.
These tide modelling tools and tide models underpin DEA products including DEA Coastlines and DEA Intertidal.
The notebook demonstrates how to:
Model tide heights for specific coordinates and times using the
model_tidesfunctionModel tide heights for each satellite observation using the
tidal_tagfunctionUse tide height data to produce median composites of the coast at low and high tide
Swap a dataset’s dimensions to make it easier to select imagery from low to high tide.
Compute ebb or flow tide phase data to determine whether water levels were rising or falling in each satellite observation
Advanced tools:
Spatially model tides into each pixel of a satellite dataset using
pixel_tidesEvaluate potential biases in the tides observed by a satellite using
tidal_stats
Getting started
To run this analysis, run all the cells in the notebook, starting with the “Load packages” cell.
Load packages
[1]:
import datacube
import xarray as xr
import pandas as pd
import matplotlib.pyplot as plt
from datacube.utils.masking import mask_invalid_data
import sys
sys.path.insert(1, "../Tools/")
from dea_tools.datahandling import load_ard
from dea_tools.plotting import rgb, display_map
from dea_tools.coastal import model_tides, tidal_tag, pixel_tides, tidal_stats
Connect to the datacube
[2]:
dc = datacube.Datacube(app="Tidal_modelling")
Modelling tide heights using model_tides
To simply model tide heights for a specific location and set of times, we can use the dea_tools.coastal.model_tides function. For example, we can model hourly tides across a one month period (September 2022):
[3]:
# Set of times to model tides for
date_list = pd.date_range(start="2022-09-01", end="2022-09-10", freq="1h")
# Run the FES2014 tidal model
tide_df = model_tides(
x=[122.21],
y=[-18.20],
time=date_list,
)
# Print outputs
tide_df.head()
Modelling tides using FES2014
[3]:
| tide_model | tide_m | |||
|---|---|---|---|---|
| time | x | y | ||
| 2022-09-01 00:00:00 | 122.21 | -18.2 | FES2014 | -3.606788 |
| 2022-09-01 01:00:00 | 122.21 | -18.2 | FES2014 | -2.470168 |
| 2022-09-01 02:00:00 | 122.21 | -18.2 | FES2014 | -0.675034 |
| 2022-09-01 03:00:00 | 122.21 | -18.2 | FES2014 | 1.140802 |
| 2022-09-01 04:00:00 | 122.21 | -18.2 | FES2014 | 2.591887 |
Tide heights for each time and coordinate are included in the tide_m column above (representing tide height in metres relative to Mean Sea Level).
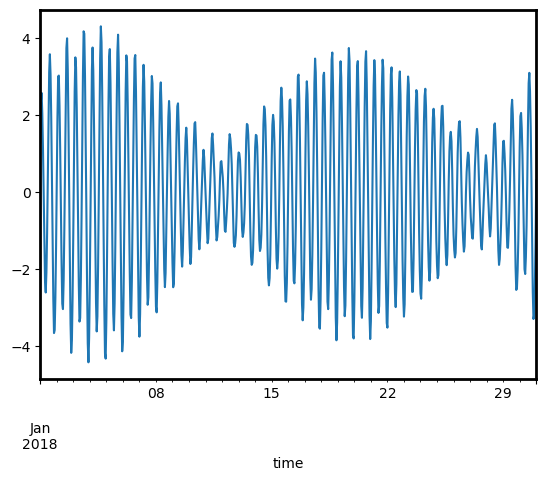
We can also plot out resulting tides to view how tides changed across this month. By looking at the y-axis, we can see that tides ranged from a minimum of ~-4 metres up to a maximum of +4 metres relative to Mean Sea Level:
[4]:
tide_df.reset_index(["x", "y"]).tide_m.plot();
“One-to-many” and “one-to-one” modes
By default, the model_tides function operates in “one-to-many” mode, which will model tides for every requested timestep, at every requested location. For example, if we provided five x, y coordinates and five timesteps, the function would return:
5 locations * 5 timesteps = 25 modelled tides
However, often you may have a list of locations and matching timesteps. Using “one-to-one” mode, we can model tides for only these exact pairs of locations and times:
5 timesteps at 5 locations = 5 modelled tides
To demonstrate “one-to-one” mode, imagine we have a pandas.Dataframe where each row contains unique site locations and times:
[5]:
sites_df = pd.DataFrame({
"time": pd.date_range(start="2022-09-01", end="2022-09-30", periods=5),
"x": [122.21, 122.22, 122.23, 122.24, 122.25],
"y": [-18.20, -18.20, -18.20, -18.20, -18.20]
})
sites_df
[5]:
| time | x | y | |
|---|---|---|---|
| 0 | 2022-09-01 00:00:00 | 122.21 | -18.2 |
| 1 | 2022-09-08 06:00:00 | 122.22 | -18.2 |
| 2 | 2022-09-15 12:00:00 | 122.23 | -18.2 |
| 3 | 2022-09-22 18:00:00 | 122.24 | -18.2 |
| 4 | 2022-09-30 00:00:00 | 122.25 | -18.2 |
Using “one-to-one” mode, we can model a tide height for each row in our dataframe, and add it as a new dataframe column:
[6]:
# Model tides in "one-to-one" mode
tide_df = model_tides(
x=sites_df.x,
y=sites_df.y,
time=sites_df.time,
mode="one-to-one",
)
# Add results as a new datframe column
sites_df["tide_height"] = tide_df.tide_m.values
sites_df.style.set_properties(**{"background-color": "#FFFF8F"}, subset=["tide_height"])
Modelling tides using FES2014 in parallel
100%|██████████| 5/5 [00:12<00:00, 2.54s/it]
[6]:
| time | x | y | tide_height | |
|---|---|---|---|---|
| 0 | 2022-09-01 00:00:00 | 122.210000 | -18.200000 | -3.606788 |
| 1 | 2022-09-08 06:00:00 | 122.220000 | -18.200000 | -1.738778 |
| 2 | 2022-09-15 12:00:00 | 122.230000 | -18.200000 | -3.303217 |
| 3 | 2022-09-22 18:00:00 | 122.240000 | -18.200000 | -0.859731 |
| 4 | 2022-09-30 00:00:00 | 122.250000 | -18.200000 | -3.687130 |
Modelling tide heights for each satellite observation using tidal_tag
However, often it is valuable to estimate the height of the tide at the exact moment satellite images were taken over a coastline. This can help sort and filter images by tide height, allowing us to learn more about how coastal environments respond to the effect of changing tides.
To demonstrate how this can be done, we first need to load in an example time series of satellite imagery.
Set up data query
First we set up a query to define the area, time period and other parameters required for loading data. In this example, we will load several years of Landsat 8 data for intertidal mud flats south of Broome in Western Australia. We load the 'nbart_red', 'nbart_green', 'nbart_blue' bands so that we can plot the data as true colour imagery.
The
dask_chunksparameter allows us to use Dask to lazily load data rather than load data directly into memory, which can take a long time and large amounts of memory. Lazy loading can be a very useful approach for when you need to load large amounts of data without crashing your analysis. In coastal applications, it allows us to load (using either.compute()or by plotting our data) only a small subset of observations from our entire time series (e.g. only low or high tide observations) without having to load the entire dataset into memory first, which can greatly decrease processing times.For more information about using Dask, refer to the Parallel processing with Dask notebook.
[7]:
# Set up data load query
query = {
"x": (122.15, 122.26),
"y": (-18.14, -18.24),
"time": ("2020-01", "2020-06"),
"measurements": ["nbart_red", "nbart_green", "nbart_blue"],
"group_by": "solar_day",
"dask_chunks": {},
}
We can preview the area that we will load data for:
[8]:
display_map(x=query['x'], y=query['y'])
[8]:
Load satellite time-series
To obtain some satellite data to analyse, we use the load_ard function to import a time series of Landsat 8 observations as an xarray.Dataset. The input data does not need to be from Landsat: any remotely-sensed imagery with timestamps and spatial coordinates provide enough data to run the tidal model.
[9]:
# Load available data from Landsat 8
ds = load_ard(
dc=dc,
products=["ga_ls8c_ard_3"],
mask_pixel_quality=False,
cloud_cover=(0, 10), # load only scenes with <10% cloud
**query
)
# Set nodata to NaN and print output
ds = mask_invalid_data(ds)
ds
Finding datasets
ga_ls8c_ard_3
Returning 13 time steps as a dask array
[9]:
<xarray.Dataset> Size: 26MB
Dimensions: (time: 13, y: 398, x: 415)
Coordinates:
* time (time) datetime64[ns] 104B 2020-01-13T01:49:41.792637 ... 20...
* y (y) float64 3kB -1.977e+06 -1.977e+06 ... -1.989e+06 -1.989e+06
* x (x) float64 3kB -1.041e+06 -1.041e+06 ... -1.029e+06 -1.029e+06
spatial_ref int32 4B 3577
Data variables:
nbart_red (time, y, x) float32 9MB dask.array<chunksize=(1, 398, 415), meta=np.ndarray>
nbart_green (time, y, x) float32 9MB dask.array<chunksize=(1, 398, 415), meta=np.ndarray>
nbart_blue (time, y, x) float32 9MB dask.array<chunksize=(1, 398, 415), meta=np.ndarray>
Attributes:
crs: EPSG:3577
grid_mapping: spatial_ref“Tagging” each satellite image with tide height metadata
We can now use the tidal_tag function from dea_tools.coastal to “tag” or associate each satellite observation in our time series with a tide height relative to mean sea level (i.e. approximately equivalent to the Australian Height Datum or AHD). This function uses the time and date of acquisition and the geographic location of each satellite observation as inputs to the Finite Element Solution 2014 (FES2014) tidal
model:
FES2014 is the last version of the FES (Finite Element Solution) tide model developed in 2014-2016. It is an improved version of the FES2012 model. This new FES2014 model has been developed, implemented and validated by the LEGOS, NOVELTIS and CLS, within a CNES funded project. FES2014 takes advantage of longer altimeter time series and better altimeter standards, improved modelling and data assimilation techniques, a more accurate ocean bathymetry and a refined mesh in most of the shallow water regions. Special efforts have been dedicated to address the major non-linear tides issue and to the determination of accurate tidal currents.
The function will automatically select a tide modelling location based on the dataset centroid. It will then output modelled tide heights as a new tide_m variable in the xarray.Dataset (the variable should appear under Data variables below):
[10]:
# Model tide heights
ds_tidal = tidal_tag(ds)
# Print output data
ds_tidal
Setting tide modelling location from dataset centroid: 122.20, -18.19
Modelling tides using FES2014
[10]:
<xarray.Dataset> Size: 26MB
Dimensions: (time: 13, y: 398, x: 415)
Coordinates:
* time (time) datetime64[ns] 104B 2020-01-13T01:49:41.792637 ... 20...
* y (y) float64 3kB -1.977e+06 -1.977e+06 ... -1.989e+06 -1.989e+06
* x (x) float64 3kB -1.041e+06 -1.041e+06 ... -1.029e+06 -1.029e+06
spatial_ref int32 4B 3577
Data variables:
nbart_red (time, y, x) float32 9MB dask.array<chunksize=(1, 398, 415), meta=np.ndarray>
nbart_green (time, y, x) float32 9MB dask.array<chunksize=(1, 398, 415), meta=np.ndarray>
nbart_blue (time, y, x) float32 9MB dask.array<chunksize=(1, 398, 415), meta=np.ndarray>
tide_m (time) float32 52B 0.5622 -0.9301 1.639 ... -1.419 3.05 -2.026
Attributes:
crs: EPSG:3577
grid_mapping: spatial_refWe can easily plot this new variable to inspect the range of tide heights observed by the satellites in our time series. In this example, our observed tide heights range from approximately -2.0 to 4.0 m relative to Mean Sea Level:
[11]:
ds_tidal.tide_m.plot();
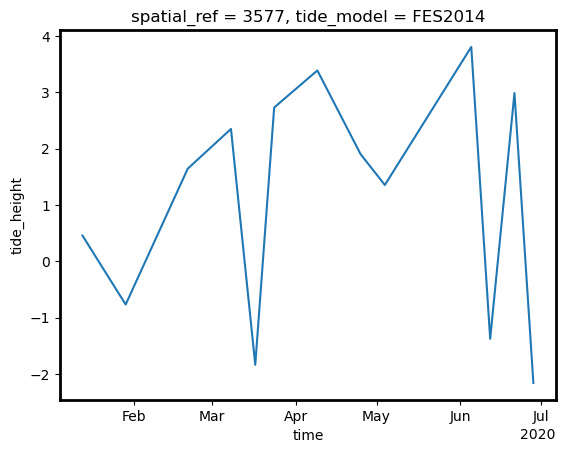
Example tide height analysis
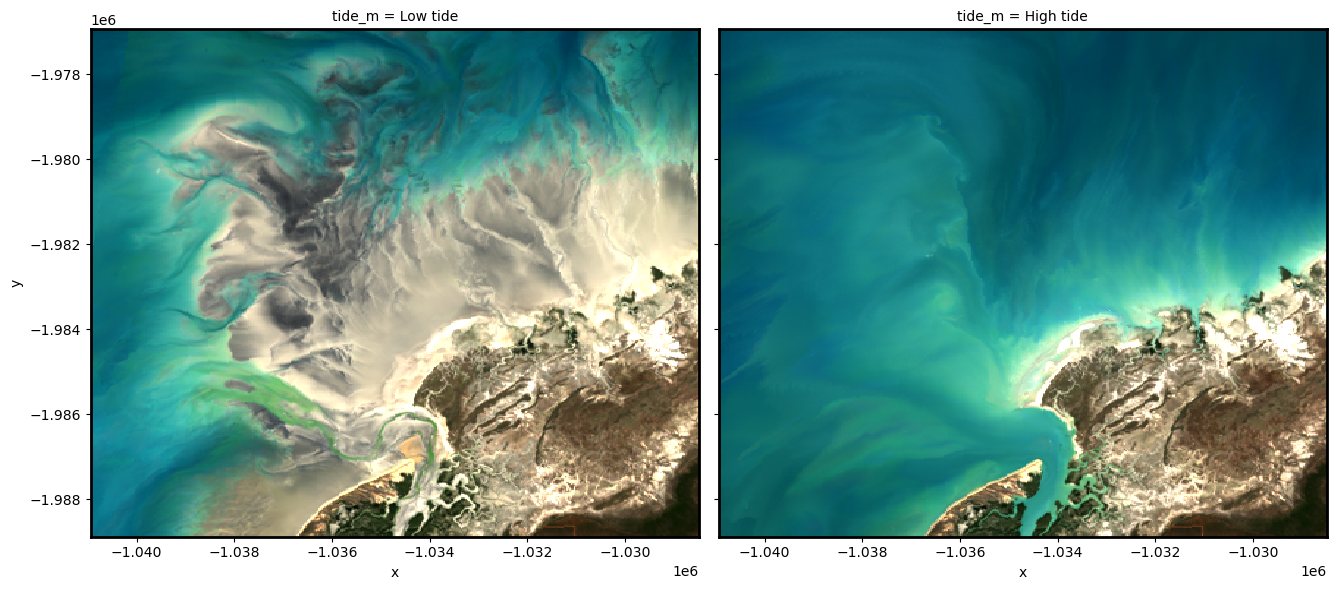
To demonstrate how tidally tagged images can be used to produce composites of high and low tide imagery, we can compute the lowest 20% and highest 20% of tide heights, and use these to filter our observations. We can then combine and plot these filtered observations to visualise how the landscape appears at low and high tide:
[12]:
# Calculate the lowest and highest 20% of tides
lowest_20, highest_20 = ds_tidal.tide_m.quantile([0.2, 0.8]).values
# Filter our data to low and high tide observations
filtered_low = ds_tidal.where(ds_tidal.tide_m <= lowest_20, drop=True)
filtered_high = ds_tidal.where(ds_tidal.tide_m >= highest_20, drop=True)
# Take the simple median of each set of low and high tide observations to
# produce a composite (alternatively, observations could be combined
# using a geomedian to keep band relationships consistent)
median_low = filtered_low.median(dim="time", keep_attrs=True)
median_high = filtered_high.median(dim="time", keep_attrs=True)
# Combine low and high tide medians into a single dataset and give
# each layer a meaningful name
ds_highlow = xr.concat([median_low, median_high], dim="tide_m")
ds_highlow["tide_m"] = ["Low tide", "High tide"]
# Plot low and high tide medians side-by-side
rgb(ds_highlow, col="tide_m")
/env/lib/python3.10/site-packages/rasterio/warp.py:344: NotGeoreferencedWarning: Dataset has no geotransform, gcps, or rpcs. The identity matrix will be returned.
_reproject(
Swapping dimensions
The tidal_tag function allows you to use tide heights as the primary dimension in the dataset, rather than time. Setting swap_dims=True will swap the time dimension in the original xarray.Dataset to the new tide_m variable.
[13]:
# Model tide heights
ds_tidal = tidal_tag(ds, swap_dims=True)
# Print output data
ds_tidal
Setting tide modelling location from dataset centroid: 122.20, -18.19
Modelling tides using FES2014
[13]:
<xarray.Dataset> Size: 26MB
Dimensions: (y: 398, x: 415, tide_m: 13)
Coordinates:
* y (y) float64 3kB -1.977e+06 -1.977e+06 ... -1.989e+06 -1.989e+06
* x (x) float64 3kB -1.041e+06 -1.041e+06 ... -1.029e+06 -1.029e+06
spatial_ref int32 4B 3577
* tide_m (tide_m) float32 52B -2.026 -1.811 -1.419 ... 3.05 3.272 3.786
Data variables:
nbart_red (tide_m, y, x) float32 9MB dask.array<chunksize=(1, 398, 415), meta=np.ndarray>
nbart_green (tide_m, y, x) float32 9MB dask.array<chunksize=(1, 398, 415), meta=np.ndarray>
nbart_blue (tide_m, y, x) float32 9MB dask.array<chunksize=(1, 398, 415), meta=np.ndarray>
Attributes:
crs: EPSG:3577
grid_mapping: spatial_refThe dataset now contains three dimensions: tide_m, x and y. This can make it easier to analyse the data with respect to tide, e.g. plotting the lowest and highest tide image in our dataset:
[14]:
# Plot first (lowest tide) and last (highest tide) images
rgb(ds_tidal, index_dim="tide_m", index=[0, -1])
Note: The white dots in the images above are false positives in the automated cloud mask caused by bright sandy shorelines being mistaken for clouds.
Modelling ebb and flow tidal phases
The tidal_tag function also allows us to determine whether each satellite observation was taken while the tide was rising/incoming (flow tide) or falling/outgoing (ebb tide) by setting ebb_flow=True. This is achieved by comparing tide heights 15 minutes before and after the observed satellite observation.
Ebb and flow data can provide valuable contextual information for interpreting satellite imagery, particularly in tidal flat or mangrove forest environments where water may remain in the landscape for considerable time after the tidal peak.
[15]:
# Model tide heights
ds_tidal = tidal_tag(ds, ebb_flow=True)
# Print output data
ds_tidal
Setting tide modelling location from dataset centroid: 122.20, -18.19
Modelling tides using FES2014
Modelling tidal phase (e.g. ebb or flow)
Modelling tides using FES2014
[15]:
<xarray.Dataset> Size: 26MB
Dimensions: (time: 13, y: 398, x: 415)
Coordinates:
* time (time) datetime64[ns] 104B 2020-01-13T01:49:41.792637 ... 20...
* y (y) float64 3kB -1.977e+06 -1.977e+06 ... -1.989e+06 -1.989e+06
* x (x) float64 3kB -1.041e+06 -1.041e+06 ... -1.029e+06 -1.029e+06
spatial_ref int32 4B 3577
Data variables:
nbart_red (time, y, x) float32 9MB dask.array<chunksize=(1, 398, 415), meta=np.ndarray>
nbart_green (time, y, x) float32 9MB dask.array<chunksize=(1, 398, 415), meta=np.ndarray>
nbart_blue (time, y, x) float32 9MB dask.array<chunksize=(1, 398, 415), meta=np.ndarray>
tide_m (time) float32 52B 0.5622 -0.9301 1.639 ... -1.419 3.05 -2.026
ebb_flow (time) <U4 208B 'Flow' 'Flow' 'Flow' ... 'Flow' 'Flow' 'Flow'
Attributes:
crs: EPSG:3577
grid_mapping: spatial_refWe now have data giving us the both the tide height and tidal phase (‘ebb’ or ‘flow’) for every satellite image:
[16]:
ds_tidal[["time", "tide_m", "ebb_flow"]].to_dataframe().drop("spatial_ref", axis=1)
[16]:
| tide_m | ebb_flow | |
|---|---|---|
| time | ||
| 2020-01-13 01:49:41.792637 | 0.562249 | Flow |
| 2020-01-29 01:49:37.148233 | -0.930141 | Flow |
| 2020-02-21 01:55:18.216005 | 1.639398 | Flow |
| 2020-03-08 01:55:12.515274 | 2.301430 | Flow |
| 2020-03-17 01:49:21.317513 | -1.811296 | Flow |
| 2020-03-24 01:55:04.353944 | 2.813786 | Flow |
| 2020-04-09 01:54:56.077227 | 3.272171 | Flow |
| 2020-04-25 01:54:48.941936 | 2.010019 | Flow |
| 2020-05-04 01:48:56.906589 | 1.238869 | Ebb |
| 2020-06-05 01:49:03.396612 | 3.785858 | Flow |
| 2020-06-12 01:54:54.641568 | -1.419148 | Flow |
| 2020-06-21 01:49:12.757339 | 3.050224 | Flow |
| 2020-06-28 01:55:03.091663 | -2.025774 | Flow |
We could for example use this data to filter our observations to keep ebbing phase observations only:
[17]:
ds_tidal.where(ds_tidal.ebb_flow == "Ebb", drop=True)
[17]:
<xarray.Dataset> Size: 2MB
Dimensions: (time: 1, y: 398, x: 415)
Coordinates:
* time (time) datetime64[ns] 8B 2020-05-04T01:48:56.906589
* y (y) float64 3kB -1.977e+06 -1.977e+06 ... -1.989e+06 -1.989e+06
* x (x) float64 3kB -1.041e+06 -1.041e+06 ... -1.029e+06 -1.029e+06
spatial_ref int32 4B 3577
Data variables:
nbart_red (time, y, x) float32 661kB dask.array<chunksize=(1, 398, 415), meta=np.ndarray>
nbart_green (time, y, x) float32 661kB dask.array<chunksize=(1, 398, 415), meta=np.ndarray>
nbart_blue (time, y, x) float32 661kB dask.array<chunksize=(1, 398, 415), meta=np.ndarray>
tide_m (time) float32 4B 1.239
ebb_flow (time) object 8B 'Ebb'
Attributes:
crs: EPSG:3577
grid_mapping: spatial_refAdvanced
Modelling tides for each pixel in a satellite time series using pixel_tides
The previous examples show how to model a single tide height for each satellite image using the centroid of the image as a tide modelling location. However, in reality tides vary spatially, potentially up to several metres across a distance of kilometres in areas of complex tidal dynamics. This means that an individual satellite image can contain a range of tide height conditions.
To capture this spatial variability in tide heights, we can use the pixel_tides function from dea_tools.coastal. For efficient processing, this function first models tides into a low resolution 5000 m grid surrounding each satellite image in our time series. This lower resolution data will also include a buffer around the extent of our data tides can be modelled seamlessly across analysis boundaries:
[18]:
# Extract a subset of our satellite data above to make plotting easier
ds_subset = ds.isel(time=slice(0, 3))
# Model tides spatially using `pixel_tides`
tides_lowres = pixel_tides(ds_subset, resample=False)
Creating reduced resolution 5000 x 5000 metre tide modelling array
Modelling tides using FES2014 in parallel
100%|██████████| 5/5 [00:12<00:00, 2.49s/it]
Returning low resolution tide array
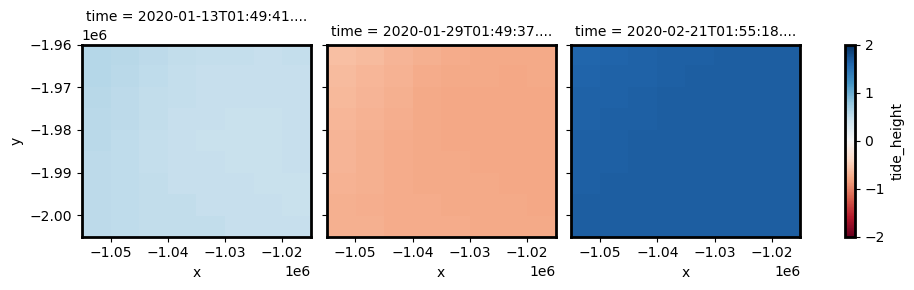
If we plot the resulting data, we can see that we now have 2D tide surfaces for each timestep in our data (instead of the single tide height per timestamp returned by the tidal_tag function).
Blue values below indicate low tide pixels, while red indicates high tide pixels. If you look closely at the second and third timestep below, you may also be able to see some spatial variability in tide heights within each timestep, with slight variations in tide heights along the left (west) side of the study area:
[19]:
tides_lowres.plot.imshow(col="time", vmin=-1, vmax=1, cmap='RdBu')
[19]:
<xarray.plot.facetgrid.FacetGrid at 0x7f971049b250>
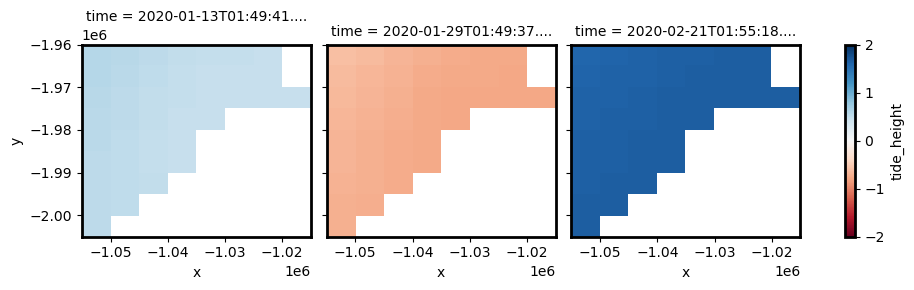
Reprojecting tide heights back into original high resolution spatial grid
By setting resample=True, we can use interpolation to re-project our low resolution tide data back into the resolution of our satellite image, resulting in an individual tide height value for every single pixel in our dataset through time and space:
[20]:
# Model tides spatially using `pixel_tides`
tides_highres, tides_lowres = pixel_tides(ds_subset, resample=True)
tides_highres.plot.imshow(col="time", vmin=-1, vmax=1, cmap="RdBu")
Creating reduced resolution 5000 x 5000 metre tide modelling array
Modelling tides using FES2014 in parallel
100%|██████████| 5/5 [00:12<00:00, 2.59s/it]
Reprojecting tides into original array
[20]:
<xarray.plot.facetgrid.FacetGrid at 0x7f97108df190>
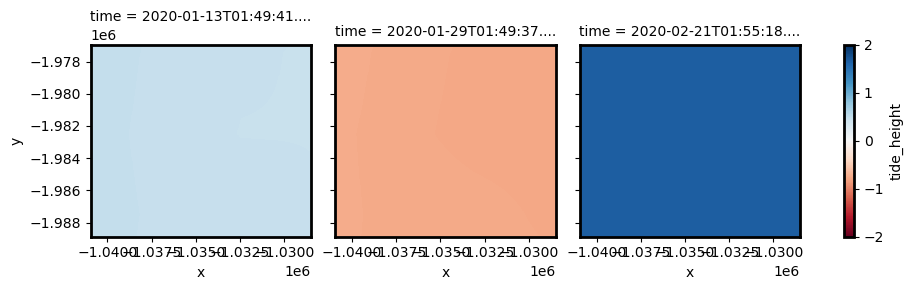
tides_highres will have exactly the same dimensions as ds_subset, with a unique tide height for every satellite pixel:
[21]:
ds_subset.sizes
[21]:
Frozen({'time': 3, 'y': 398, 'x': 415})
[22]:
tides_highres.sizes
[22]:
Frozen({'time': 3, 'y': 398, 'x': 415})
Because of this, our stack of tides can be added as an additional 3D variable in our dataset:
[23]:
ds_subset["tide_m"] = tides_highres
ds_subset
[23]:
<xarray.Dataset> Size: 8MB
Dimensions: (time: 3, y: 398, x: 415)
Coordinates:
* time (time) datetime64[ns] 24B 2020-01-13T01:49:41.792637 ... 202...
* y (y) float64 3kB -1.977e+06 -1.977e+06 ... -1.989e+06 -1.989e+06
* x (x) float64 3kB -1.041e+06 -1.041e+06 ... -1.029e+06 -1.029e+06
spatial_ref int32 4B 3577
tide_model <U7 28B 'FES2014'
Data variables:
nbart_red (time, y, x) float32 2MB dask.array<chunksize=(1, 398, 415), meta=np.ndarray>
nbart_green (time, y, x) float32 2MB dask.array<chunksize=(1, 398, 415), meta=np.ndarray>
nbart_blue (time, y, x) float32 2MB dask.array<chunksize=(1, 398, 415), meta=np.ndarray>
tide_m (time, y, x) float32 2MB 0.5856 0.5854 0.5853 ... 1.638 1.638
ebb_flow (time) <U4 48B 'Flow' 'Flow' 'Flow'
Attributes:
crs: EPSG:3577
grid_mapping: spatial_refCalculating min/max/median/quantiles of tide heights for each pixel
Min, max or any specific quantile of all tide heights observed over a region can be calculated for each pixel by passing in a list of quantiles/percentiles.
This calculation is performed on the low resolution modelled tide data before reprojecting to higher resolution, so should be faster than calculating min/max/median tide at high resolution:
[24]:
tides_highres_quantiles, tides_lowres_quantiles = pixel_tides(
ds_subset, resample=True, calculate_quantiles=(0, 0.5, 1)
)
Creating reduced resolution 5000 x 5000 metre tide modelling array
Modelling tides using FES2014 in parallel
100%|██████████| 5/5 [00:12<00:00, 2.54s/it]
Computing tide quantiles
Reprojecting tides into original array
[25]:
tides_highres_quantiles.plot.imshow(col="quantile")
[25]:
<xarray.plot.facetgrid.FacetGrid at 0x7f9711d4bac0>
Pixel-based tides for custom times
Instead of using times contained in the time dimension of our dataset, we can also calculate pixel-based tides for a custom set of times:
[26]:
custom_times = pd.date_range(start="2022-01-01", end="2022-01-02", freq="6H")
tides_highres, tides_lowres = pixel_tides(ds_subset, resample=True, times=custom_times)
Creating reduced resolution 5000 x 5000 metre tide modelling array
Modelling tides using FES2014 in parallel
100%|██████████| 5/5 [00:12<00:00, 2.58s/it]
Reprojecting tides into original array
[27]:
tides_highres.plot.imshow(col="time")
[27]:
<xarray.plot.facetgrid.FacetGrid at 0x7f970ba373a0>
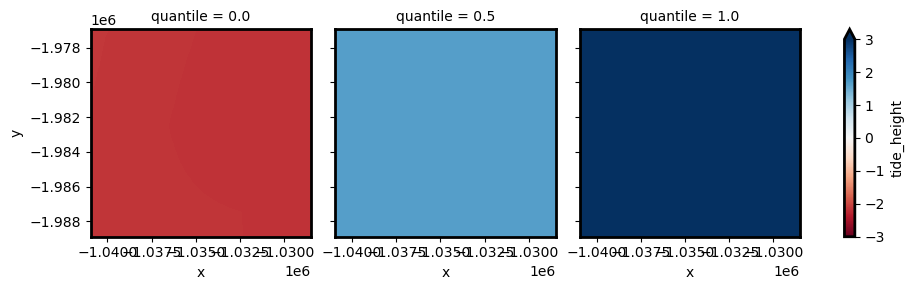
Evaluating tidal biases using tidal_stats
The complex temporal behaviour of tides mean that a sun synchronous sensor like Landsat does not observe the full range of the tidal cycle at all locations. Biases in the proportion of the tidal range observed by satellites can prevent us from obtaining data on areas of the coastline exposed or inundated at the extremes of the tidal range. This can risk gaining misleading insights into the true extent of the area of the coastline affected by tides, and make it difficult to compare high or low tide images fairly in different locations.
The tidal_stats function can assist in evaluating how the range of tides observed by satellites compare to the full tidal range. It works by using our tidal model to to model all available tide heights at a regular interval (every two hours by default) across the entire time period covered by the input satellite time series dataset. This is then compared against the tide heights in observed by the satellite and used to calculate a range of statistics and a plot that summarises potential
biases in the data.
For a more detailed discussion of the issue of tidal bias in sun-synchronous satellite observations of the coastline, refer to the ‘Limitations and future work’ section in Bishop-Taylor et al. 2018.
[28]:
out_stats = tidal_stats(ds)
Setting tide modelling location from dataset centroid: 122.20, -18.19
Modelling tides using FES2014
Modelling tides using FES2014
tide_model tide_m
time x y
2020-01-13 01:49:41.792637 122.204971 -18.190029 FES2014 0.562249
2020-01-13 03:49:41.792637 122.204971 -18.190029 FES2014 3.454227
2020-01-13 05:49:41.792637 122.204971 -18.190029 FES2014 2.493470
2020-01-13 07:49:41.792637 122.204971 -18.190029 FES2014 -0.528646
2020-01-13 09:49:41.792637 122.204971 -18.190029 FES2014 -3.204748
... ... ...
2020-06-27 17:49:41.792637 122.204971 -18.190029 FES2014 1.922974
2020-06-27 19:49:41.792637 122.204971 -18.190029 FES2014 2.180105
2020-06-27 21:49:41.792637 122.204971 -18.190029 FES2014 0.217506
2020-06-27 23:49:41.792637 122.204971 -18.190029 FES2014 -1.491524
2020-06-28 01:49:41.792637 122.204971 -18.190029 FES2014 -2.060531
[2005 rows x 2 columns]
59% of the 9.81 m modelled astronomical tidal range is observed at this location.
The lowest 28% and highest 12% of astronomical tides are never observed.
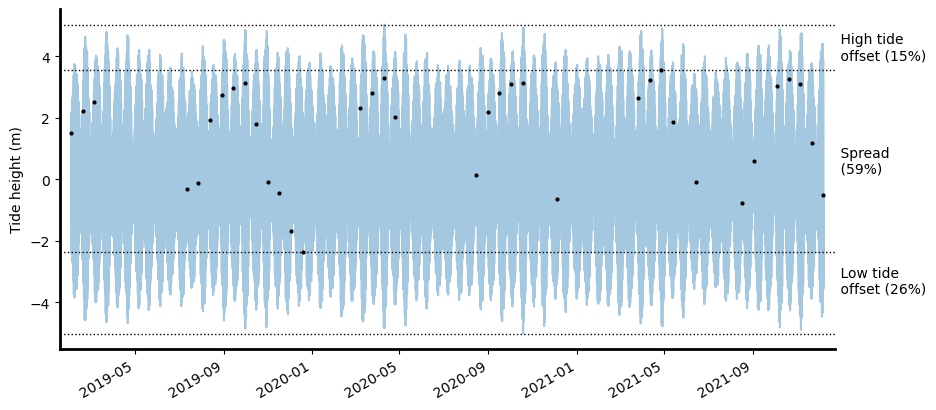
The function also outputs a pandas.Series object containing a set of statistics that compare the observed vs. full modelled tidal ranges. These statistics include:
tidepost_lat: latitude used for modelling tide heights
tidepost_lon: longitude used for modelling tide heights
observed_min_m: minimum tide height observed by the satellite (in metre units)
all_min_m: minimum tide height from full modelled tidal range (in metre units)
observed_max_m: maximum tide height observed by the satellite (in metre units)
all_max_m: maximum tide height from full modelled tidal range (in metre units)
observed_range_m: tidal range observed by the satellite (in metre units)
all_range_m: full modelled tidal range (in metre units)
spread_m: proportion of the full modelled tidal range observed by the satellite (see Bishop-Taylor et al. 2018)
low_tide_offset: proportion of the lowest tides never observed by the satellite (see Bishop-Taylor et al. 2018)
high_tide_offset: proportion of the highest tides never observed by the satellite (see Bishop-Taylor et al. 2018)
[29]:
out_stats
[29]:
tidepost_lat -18.190
tidepost_lon 122.205
observed_mean_m 1.114
all_mean_m 0.001
observed_min_m -2.026
all_min_m -4.803
observed_max_m 3.786
all_max_m 5.008
observed_range_m 5.812
all_range_m 9.811
spread 0.592
low_tide_offset 0.283
high_tide_offset 0.125
dtype: float64
Additional information
FES2014: Tidal modelling is provided by the FES2014 global tidal model, implemented using functions from the pyTMD Python package. FES2014 was produced by NOVELTIS, LEGOS, CLS Space Oceanography Division and CNES. It is distributed by AVISO, with support from CNES (https://www.aviso.altimetry.fr/en/data/products/auxiliary-products/global-tide-fes/description-fes2014.html).
License: The code in this notebook is licensed under the Apache License, Version 2.0. Digital Earth Australia data is licensed under the Creative Commons by Attribution 4.0 license.
Contact: If you need assistance, please post a question on the Open Data Cube Slack channel or on the GIS Stack Exchange using the open-data-cube tag (you can view previously asked questions here). If you would like to report an issue with this notebook, you can file one on
GitHub.
Last modified: July 2024
Compatible datacube version:
[30]:
print(datacube.__version__)
1.8.18
Tags
Tags: sandbox compatible, NCI compatible, landsat 8, display_map, load_ard, rgb, tidal_tag, tidal_stats, model_tides, pixel_tides, tide modelling, intertidal, Dask, lazy loading, rolling window