Vegetation phenology 
Sign up to the DEA Sandbox to run this notebook interactively from a browser
Compatibility: Notebook currently compatible with both the
NCIandDEA SandboxenvironmentsProducts used: ga_s2am_ard_3, ga_s2bm_ard_3
Background
Phenology is the study of plant and animal life cycles in the context of the seasons. It can be useful in understanding the life cycle trends of crops and how the growing seasons are affected by changes in climate. For more information, see the USGS page on deriving phenology from NDVI time-series
Description
This notebook demonstrates how to calculate vegetation phenology statistics using the DEA function xr_phenology. To detect changes in plant life using satellite images, the script uses either the Normalized Difference Vegetation Index (NDVI) or the Enhanced Vegetation Index (EVI), which are common proxies for vegetation growth and health.
The outputs of this notebook can be used to assess spatio-temporal differences in the growing seasons of agriculture fields or native vegetation.
This notebook demonstrates the following steps:
Load cloud-masked Sentinel 2 data for an area of interest.
Calculate a vegetation proxy index (NDVI or EVI).
Generate a zonal time series of vegetation health
Complete and smooth the vegetation timeseries to remove gaps and noise.
Calculate phenology statistics on a simple 1D vegetation time series
Calculate per-pixel phenology statistics
Optional: Calculating generic temporal statistics usng the
hdstatslibrary
Getting started
To run this analysis, run all the cells in the notebook, starting with the “Load packages” cell.
Load packages
Load key Python packages and supporting functions for the analysis.
[1]:
%matplotlib inline
import os
import datacube
import numpy as np
import pandas as pd
import xarray as xr
import datetime as dt
import matplotlib.pyplot as plt
import sys
sys.path.insert(1, '../Tools/')
from dea_tools.temporal import xr_phenology, temporal_statistics
from dea_tools.datahandling import load_ard
from dea_tools.bandindices import calculate_indices
from dea_tools.plotting import display_map, rgb
from dea_tools.dask import create_local_dask_cluster
import warnings
warnings.simplefilter(action='ignore', category=FutureWarning)
# Create local dask cluster to improve data load time
client = create_local_dask_cluster(return_client=True)
Client
Client-086e1a78-adb7-11ed-9c6f-627f0658669b
| Connection method: Cluster object | Cluster type: distributed.LocalCluster |
| Dashboard: /user/robbi.bishoptaylor@ga.gov.au/proxy/8787/status |
Cluster Info
LocalCluster
3e18f142
| Dashboard: /user/robbi.bishoptaylor@ga.gov.au/proxy/8787/status | Workers: 1 |
| Total threads: 31 | Total memory: 237.21 GiB |
| Status: running | Using processes: True |
Scheduler Info
Scheduler
Scheduler-ff8c435d-cc00-466b-ae9c-47b3bebcec79
| Comm: tcp://127.0.0.1:44823 | Workers: 1 |
| Dashboard: /user/robbi.bishoptaylor@ga.gov.au/proxy/8787/status | Total threads: 31 |
| Started: Just now | Total memory: 237.21 GiB |
Workers
Worker: 0
| Comm: tcp://127.0.0.1:35389 | Total threads: 31 |
| Dashboard: /user/robbi.bishoptaylor@ga.gov.au/proxy/36433/status | Memory: 237.21 GiB |
| Nanny: tcp://127.0.0.1:36513 | |
| Local directory: /tmp/dask-worker-space/worker-5sv8yz13 | |
Connect to the datacube
Connect to the datacube so we can access DEA data. The app parameter is a unique name for the analysis which is based on the notebook file name.
[2]:
dc = datacube.Datacube(app='Vegetation_phenology')
Analysis parameters
The following cell sets important parameters for the analysis:
veg_proxy: Band index to use as a proxy for vegetation health e.g.'NDVI'or'EVI'lat: The central latitude to analyse (e.g.-10.6996).lon: The central longitude to analyse (e.g.35.2708).buffer: The number of square degrees to load around the central latitude and longitude. For reasonable loading times, set this as0.1or lower.time_range: The year range to analyse (e.g.('2019-01', '2019-06')).
[3]:
# Set the vegetation proxy to use
veg_proxy = 'NDVI'
# Define area of interest
lat = -33.3635
lon = 121.21
lon_buffer = 0.015
lat_buffer = 0.0075
# Set the range of dates for the analysis
time_range = ('2019-01-01', '2020-12-20')
[4]:
# Combine central lat,lon with buffer to get area of interest
lat_range = (lat-lat_buffer, lat+lat_buffer)
lon_range = (lon-lon_buffer, lon+lon_buffer)
View the selected location
The next cell will display the selected area on an interactive map. Feel free to zoom in and out to get a better understanding of the area you’ll be analysing. Clicking on any point of the map will reveal the latitude and longitude coordinates of that point.
[5]:
display_map(x=lon_range, y=lat_range)
[5]:
Load cloud-masked Sentinel-2 data
The first step is to load Sentinel-2 data for the specified area of interest and time range. The load_ard function is used here to load data that has been masked for cloud, shadow and quality filters, making it ready for analysis.
[6]:
# Create a reusable query
query = {
'y': lat_range,
'x': lon_range,
'time': time_range,
'measurements': ['nbart_red', 'nbart_green', 'nbart_blue', 'nbart_nir_1'],
'resolution': (-20, 20),
'output_crs': 'epsg:6933',
'group_by':'solar_day'
}
# Load available data from Sentinel-2
ds = load_ard(
dc=dc,
products=['ga_s2am_ard_3', 'ga_s2bm_ard_3'],
cloud_mask='s2cloudless',
min_gooddata=0.9,
**query,
)
# Shut down Dask client now that we have loaded the data we need
client.close()
# Preview data
ds
Finding datasets
ga_s2am_ard_3
ga_s2bm_ard_3
Counting good quality pixels for each time step using s2cloudless
Filtering to 142 out of 287 time steps with at least 90.0% good quality pixels
Applying s2cloudless pixel quality/cloud mask
Loading 142 time steps
/env/lib/python3.8/site-packages/rasterio/warp.py:344: NotGeoreferencedWarning: Dataset has no geotransform, gcps, or rpcs. The identity matrix will be returned.
_reproject(
[6]:
<xarray.Dataset>
Dimensions: (time: 142, y: 81, x: 146)
Coordinates:
* time (time) datetime64[ns] 2019-01-01T02:06:37.098000 ... 2020-12...
* y (y) float64 -4.024e+06 -4.024e+06 ... -4.026e+06 -4.026e+06
* x (x) float64 1.169e+07 1.169e+07 1.169e+07 ... 1.17e+07 1.17e+07
spatial_ref int32 6933
Data variables:
nbart_red (time, y, x) float32 1.696e+03 1.77e+03 ... 2.089e+03 2.259e+03
nbart_green (time, y, x) float32 1.283e+03 1.339e+03 ... 1.55e+03 1.69e+03
nbart_blue (time, y, x) float32 1e+03 1.057e+03 ... 1.148e+03 1.196e+03
nbart_nir_1 (time, y, x) float32 2.305e+03 2.386e+03 ... 2.806e+03
Attributes:
crs: epsg:6933
grid_mapping: spatial_refOnce the load is complete, we can plot some of the images as as a true-colour image using the rgb function.
[7]:
rgb(ds, index=[0, 80, 90, 121], col_wrap=2)

Compute band indices
This study measures the presence of vegetation through either the normalised difference vegetation index (NDVI) or the enhanced vegetation index (EVI). The index that will be used is dictated by the veg_proxy parameter that was set in the “Analysis parameters” section.
The normalised difference vegetation index (NDVI) requires the red and nir (near-infra red) bands. The formula is
The Enhanced Vegetation Index requires the red, nir and blue bands. The formula is
Both indices are available through the calculate_indices function, imported from dea_tools.bandindices. Here, we use collection='ga_s2_3' since we’re working with Sentinel-2 Collection 3 data.
[8]:
# Calculate the chosen vegetation proxy index and add it to the loaded data set
ds = calculate_indices(ds, index=veg_proxy, collection='ga_s2_3')
The vegetation proxy index should now appear as a data variable, along with the loaded measurements, in the ds object.
Plot the vegetation index over time
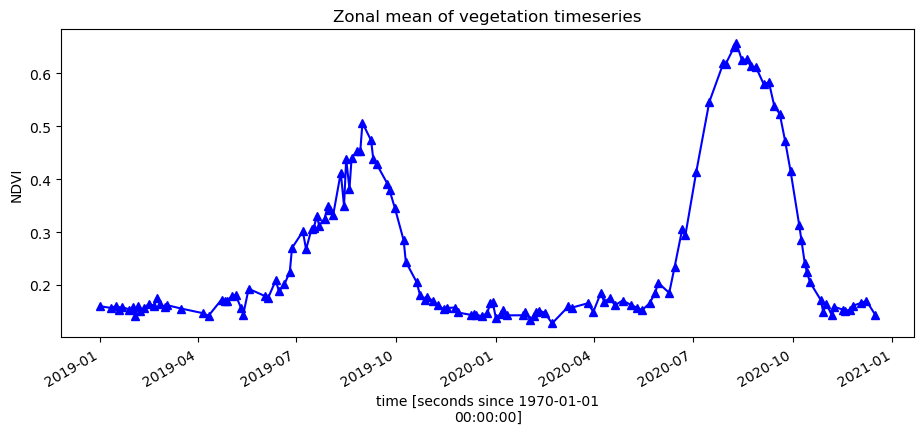
To get an idea of how the vegetation health changes throughout the year(s), we can plot a zonal time series over the region of interest. First we will do a simple plot of the zonal mean of the data.
[9]:
ds.NDVI.mean(['x', 'y']).plot.line('b-^', figsize=(11,4))
plt.title('Zonal mean of vegetation timeseries');
Smoothing/Interpolating vegetation time-series
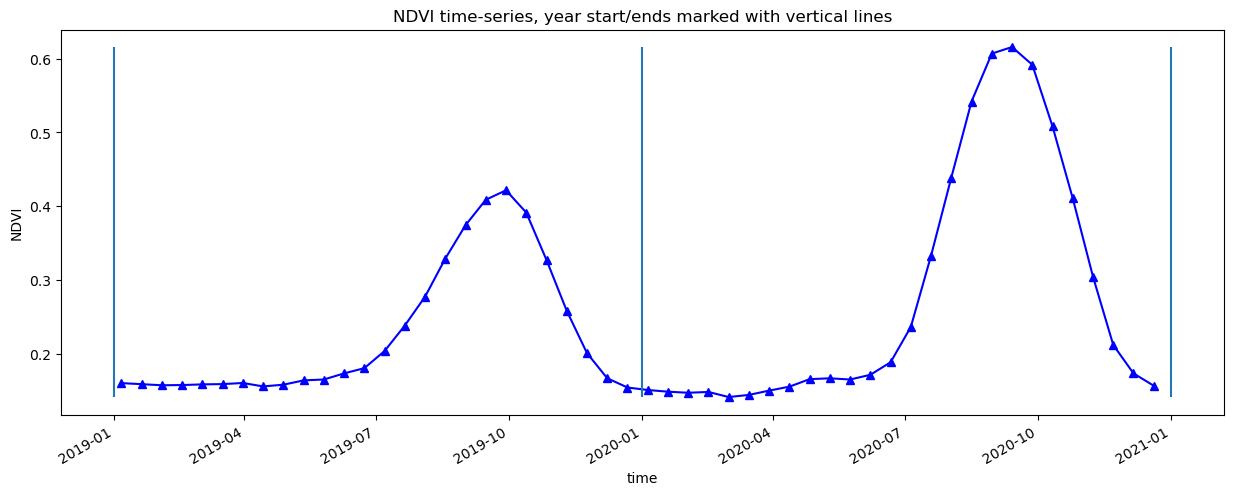
Here, we will smooth and interpolate the data to ensure we working with a consistent time-series. This is a very important step in the workflow and there are many ways to smooth, interpolate, gap-fill, remove outliers, or curve-fit the data to ensure a useable time-series. If not using the default example, you may have to define additional methods to those used here.
To do this we take two steps:
Resample the data to fortnightly time-steps using the fortnightly median
Calculate a rolling mean with a window of 4 steps
[10]:
resample_period='2W'
window=4
veg_smooth=ds[veg_proxy].resample(time=resample_period).median().rolling(time=window, min_periods=1).mean()
[11]:
veg_smooth_1D = veg_smooth.mean(['x', 'y'])
veg_smooth_1D.plot.line('b-^', figsize=(15,5))
_max=veg_smooth_1D.max()
_min=veg_smooth_1D.min()
plt.vlines(np.datetime64('2019-01-01'), ymin=_min, ymax=_max)
plt.vlines(np.datetime64('2020-01-01'), ymin=_min, ymax=_max)
plt.vlines(np.datetime64('2021-01-01'), ymin=_min, ymax=_max)
plt.title(veg_proxy+' time-series, year start/ends marked with vertical lines')
plt.ylabel(veg_proxy);
Calculate phenology statistics using xr_phenology
The DEA function xr_phenology can calculate a number of land-surface phenology statistics that together describe the characteristics of a plant’s lifecycle. The function can calculate the following statistics on either a zonal timeseries (like the one above), or on a per-pixel basis:
SOS = DOY of start of season
POS = DOY of peak of season
EOS = DOY of end of season
vSOS = Value at start of season
vPOS = Value at peak of season
vEOS = Value at end of season
Trough = Minimum value of season
LOS = Length of season (DOY)
AOS = Amplitude of season (in value units)
ROG = Rate of greening
ROS = Rate of senescence
where DOY = day-of-year (Jan 1st = 0, Dec 31st = 365). By default the function will return all the statistics as an xarray.Dataset, to return only a subset of these statistics pass a list of the desired statistics to the function e.g. stats=['SOS', 'EOS', 'ROG'].
The xr_phenology function also allows for interpolating and/or smoothing the time-series in the same way as we did above, the interpolating/smoothing will occur before the statistics are calculated.
See the dea_tools.temporal script for more information on each of the parameters in xr_phenology.
Zonal phenology statistics
To help us understand what these statistics refer too, lets first pass the simpler zonal mean (mean of all pixels in the image) time-series to the function and plot the results on the same curves as above.
First, provide a list of statistics to calculate with the parameter, pheno_stats.
method_sos : If ‘first’ then vSOS is estimated as the first positive slope on the greening side of the curve. If ‘median’, then vSOS is estimated as the median value of the postive slopes on the greening side of the curve.
method_eos : If ‘last’ then vEOS is estimated as the last negative slope on the senescing side of the curve. If ‘median’, then vEOS is estimated as the ‘median’ value of the negative slopes on the senescing side of the curve.
[12]:
pheno_stats = ['SOS','vSOS','POS','vPOS','EOS','vEOS','Trough','LOS','AOS','ROG','ROS']
method_sos = 'median'
method_eos = 'median'
Calculate phenology stats for each year in the data
[13]:
# find all the years to assist with plotting
years=veg_smooth_1D.groupby('time.year')
# get list of years in ts to help with looping
years_int=[y[0] for y in years]
#store results in dict
pheno_results = {}
#loop through years and calculate phenology
for year in years_int:
#select year
da = dict(years)[year]
#calculate stats
stats=xr_phenology(
da,
method_sos=method_sos,
method_eos=method_eos,
stats=pheno_stats,
verbose=False
)
#add results to dict
pheno_results[str(year)] = stats
for key,value in pheno_results.items():
print('Year: ' +key)
for b in value.data_vars:
print(" "+b+": ", round(float(value[b].values),3))
Year: 2019
SOS: 160.0
vSOS: 0.173
POS: 272.0
vPOS: 0.421
EOS: 314.0
vEOS: 0.258
Trough: 0.154
LOS: 154.0
AOS: 0.267
ROG: 0.002
ROS: -0.004
Year: 2020
SOS: 159.0
vSOS: 0.171
POS: 257.0
vPOS: 0.616
EOS: 313.0
vEOS: 0.304
Trough: 0.141
LOS: 154.0
AOS: 0.475
ROG: 0.005
ROS: -0.006
Plot the results with our statistcs annotated on the plot
[14]:
# find all the years to assist with plotting
years=veg_smooth_1D.groupby('time.year')
fig, ax = plt.subplots()
fig.set_size_inches(15,7)
for year, y in zip(years, years_int):
#grab tall the values we need for plotting
eos = pheno_results[str(y)].EOS.values
sos = pheno_results[str(y)].SOS.values
pos = pheno_results[str(y)].POS.values
veos = pheno_results[str(y)].vEOS.values
vsos = pheno_results[str(y)].vSOS.values
vpos = pheno_results[str(y)].vPOS.values
#create plot
#the groupby and mean below doesn't actually do anything, except allow
#the plots to be on the same x-axis. i.e. veg-data isn't modified, just time units
year[1].groupby('time.dayofyear').mean().plot(ax=ax, label=year[0])
#add start of season
ax.plot(sos, vsos, 'or')
ax.annotate('SOS',
xy=(sos, vsos),
xytext=(-15, 20),
textcoords='offset points',
arrowprops=dict(arrowstyle='-|>'))
#add end of season
ax.plot(eos, veos, 'or')
ax.annotate('EOS',
xy=(eos, veos),
xytext=(0, 20),
textcoords='offset points',
arrowprops=dict(arrowstyle='-|>'))
#add peak of season
ax.plot(pos, vpos, 'or')
ax.annotate('POS',
xy=(pos, vpos),
xytext=(-10, -25),
textcoords='offset points',
arrowprops=dict(arrowstyle='-|>'))
ax.legend()
plt.ylim(_min-0.025,_max.values+0.05)
month_abbr=['Jan','Feb','Mar','Apr','May','Jun','Jul','Aug','Sep','Oct','Nov','Dec', '']
new_m=[]
for m in month_abbr:
new_m.append(' %s'%m) #Add spaces before the month name
plt.xticks(np.linspace(0,365,13), new_m, horizontalalignment='left')
plt.xlabel('Month')
plt.ylabel(veg_proxy)
plt.title('Yearly '+veg_proxy);
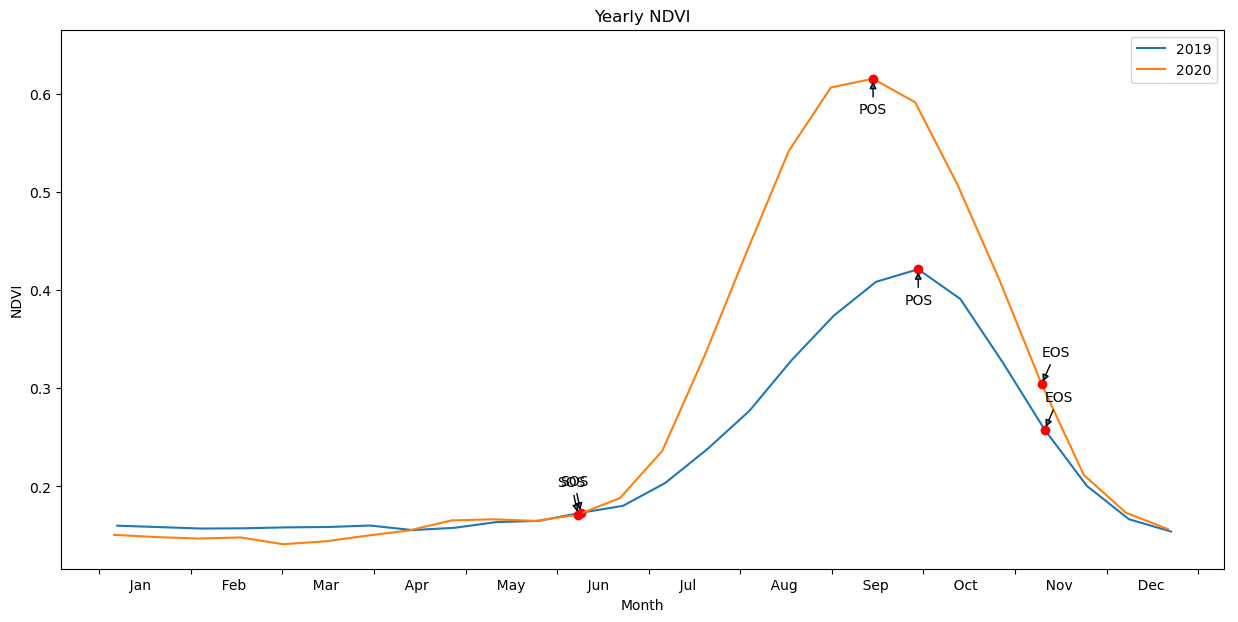
Per-pixel phenology statistics
We can now calculate the statistics for every pixel in our time-series and plot the results.
[15]:
# find all the years to assist with plotting
years=veg_smooth.groupby('time.year')
# get list of years in ts to help with looping
years_int=[y[0] for y in years]
#store results in dict
pheno_results = {}
#loop through years and calculate phenology
for year in years_int:
#select year
da = dict(years)[year]
#calculate stats
stats=xr_phenology(
da,
method_sos=method_sos,
method_eos=method_eos,
stats=pheno_stats,
verbose=False
)
#add results to dict
pheno_results[str(year)] = stats
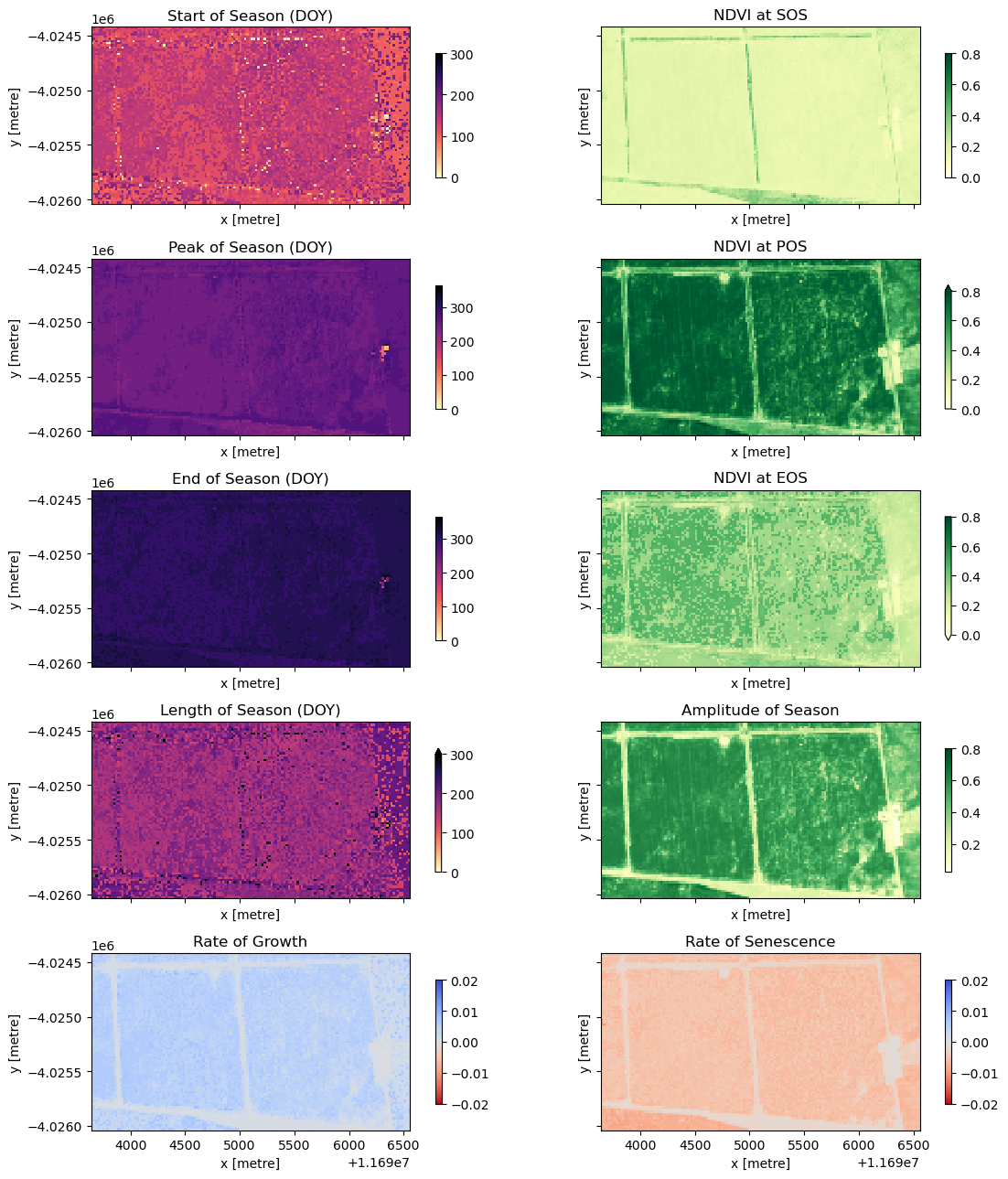
The phenology statistics have been calculated seperately for every pixel in the image. Let’s plot each of them to see the results.
Below, pick a year from the phenology results to plot.
[16]:
#Pick a year to plot
year_to_plot = '2020'
At the top if the plotting code we re-mask the phenology results with the crop-mask. This is because xr_phenologyhas methods for handling pixels with only NaNs (such as those regions outside of the polygon mask), so the results can have phenology results for regions outside the mask. We will therefore have to mask the data again.
[17]:
#select the year to plot
phen = pheno_results[year_to_plot]
# Set up figure
fig, ax = plt.subplots(nrows=5,
ncols=2,
figsize=(12, 13),
sharex=True,
sharey=True)
# Set colorbar size
cbar_size = 0.7
# Set aspect ratios
for a in fig.axes:
a.set_aspect('equal')
# Start of season
phen.SOS.plot(ax=ax[0, 0],
cmap='magma_r',
vmax=300,
vmin=0,
cbar_kwargs=dict(shrink=cbar_size, label=None))
ax[0, 0].set_title('Start of Season (DOY)')
phen.vSOS.plot(ax=ax[0, 1],
cmap='YlGn',
vmax=0.8,
vmin=0,
cbar_kwargs=dict(shrink=cbar_size, label=None))
ax[0, 1].set_title(veg_proxy + ' at SOS')
# Peak of season
phen.POS.plot(ax=ax[1, 0],
cmap='magma_r',
vmax=365,
vmin=0,
cbar_kwargs=dict(shrink=cbar_size, label=None))
ax[1, 0].set_title('Peak of Season (DOY)')
phen.vPOS.plot(ax=ax[1, 1],
cmap='YlGn',
vmax=0.8,
vmin=0,
cbar_kwargs=dict(shrink=cbar_size, label=None))
ax[1, 1].set_title(veg_proxy + ' at POS')
# End of season
phen.EOS.plot(ax=ax[2, 0],
cmap='magma_r',
vmax=365,
vmin=0,
cbar_kwargs=dict(shrink=cbar_size, label=None))
ax[2, 0].set_title('End of Season (DOY)')
phen.vEOS.plot(ax=ax[2, 1],
cmap='YlGn',
vmax=0.8,
vmin=0,
cbar_kwargs=dict(shrink=cbar_size, label=None))
ax[2, 1].set_title(veg_proxy + ' at EOS')
# Length of Season
phen.LOS.plot(ax=ax[3, 0],
cmap='magma_r',
vmax=300,
vmin=0,
cbar_kwargs=dict(shrink=cbar_size, label=None))
ax[3, 0].set_title('Length of Season (DOY)')
# Amplitude
phen.AOS.plot(ax=ax[3, 1],
cmap='YlGn',
vmax=0.8,
cbar_kwargs=dict(shrink=cbar_size, label=None))
ax[3, 1].set_title('Amplitude of Season')
# Rate of growth
phen.ROG.plot(ax=ax[4, 0],
cmap='coolwarm_r',
vmin=-0.02,
vmax=0.02,
cbar_kwargs=dict(shrink=cbar_size, label=None))
ax[4, 0].set_title('Rate of Growth')
# Rate of Sensescence
phen.ROS.plot(ax=ax[4, 1],
cmap='coolwarm_r',
vmin=-0.02,
vmax=0.02,
cbar_kwargs=dict(shrink=cbar_size, label=None))
ax[4, 1].set_title('Rate of Senescence')
plt.tight_layout();
Conclusions
In the example above, we can see these four fields are following the same cropping schedule and are therefore likely the same species of crop. We can also observe intra-field differences in the rates of growth, and in the NDVI values at different times of the season, which may be attributable to differences in soil quality, watering intensity, or other farming practices.
Phenology statistics are a powerful way to summarise the seasonal cycle of a plant’s life. Per-pixel plots of phenology can help us understand the timing of vegetation growth and sensecence across large areas and across diverse plant species as every pixel is treated as an independent series of observations. This could be important, for example, if we wanted to assess how the growing seasons are shifting as the climate warms.
Advanced: Calculating generic temporal statistics
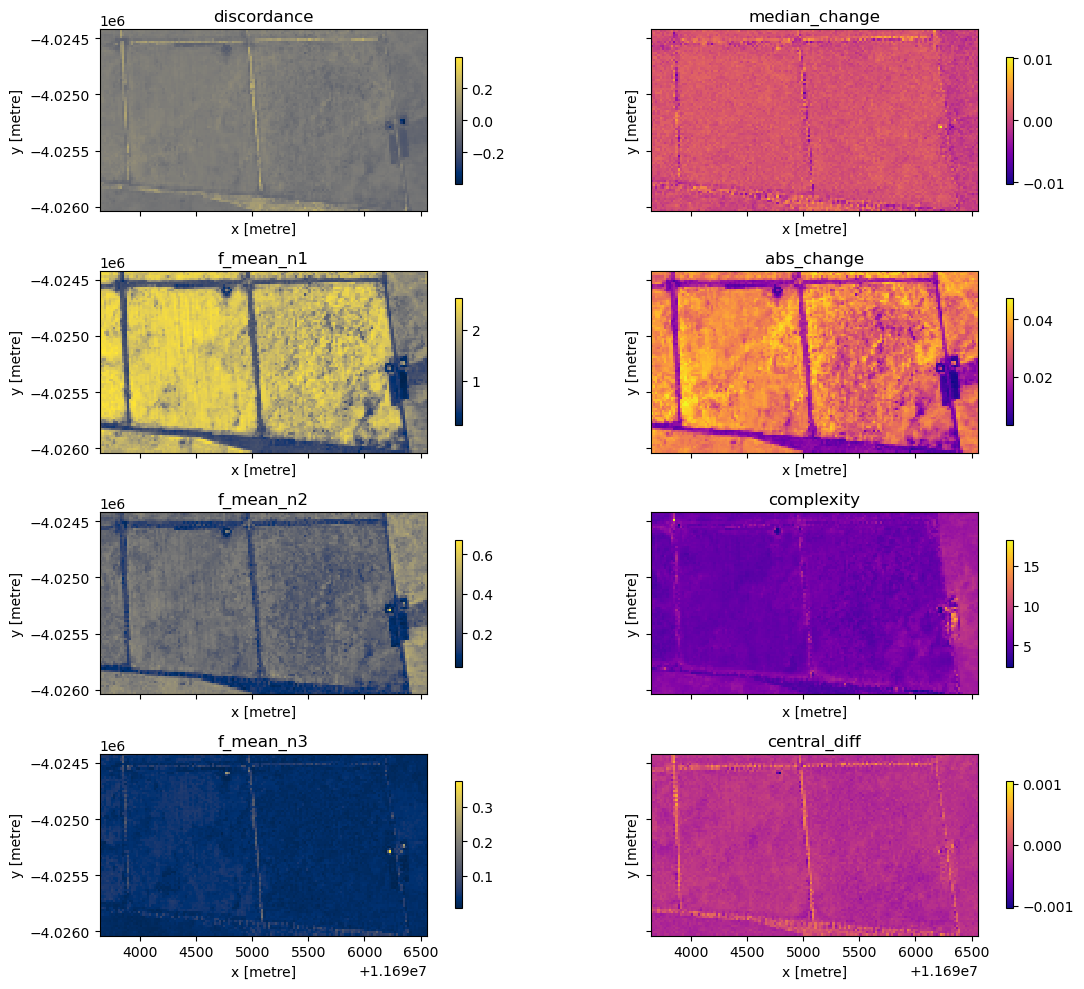
In addition to the xr_phenology function, the DEA dea_tools.temporal script contains another function for calculating generic time-series statistics, temporal_statistics. This function is built upon the hdstats library (a library of multivariate and high-dimensional statistics algorithms). This function accepts a 2 or 3D time-series of, for example, NDVI, and computes a number of summary statistics
including: - discordance - discrete fourier transform coefficients (mean, std, and median) - median change - absolute change - complexity - central difference - number of peaks (very slow to run)
Below we will calculate a number of these statistics and plot them.
[18]:
statistics = ['discordance',
'f_mean',
'median_change',
'abs_change',
'complexity',
'central_diff']
ts_stats = temporal_statistics(veg_smooth, statistics)
print(ts_stats)
Statistics:
discordance
f_mean
median_change
abs_change
complexity
central_diff
<xarray.Dataset>
Dimensions: (x: 146, y: 81)
Coordinates:
* x (x) float64 1.169e+07 1.169e+07 ... 1.17e+07 1.17e+07
* y (y) float64 -4.024e+06 -4.024e+06 ... -4.026e+06 -4.026e+06
Data variables:
discordance (y, x) float32 0.02109 0.01297 0.006562 ... -0.03446 -0.04269
f_mean_n1 (y, x) float32 2.485 2.497 2.494 2.454 ... 1.418 1.426 1.301
f_mean_n2 (y, x) float32 0.3052 0.2985 0.2995 ... 0.4116 0.4154 0.3806
f_mean_n3 (y, x) float32 0.05789 0.05444 0.05889 ... 0.02213 0.02152
median_change (y, x) float32 0.001064 0.0007725 ... -0.001186 -0.0005942
abs_change (y, x) float32 0.03746 0.03558 0.03553 ... 0.0327 0.0303
complexity (y, x) float32 4.974 4.914 4.953 5.179 ... 7.942 7.865 7.926
central_diff (y, x) float32 -0.0001038 -0.0001062 ... -0.0001837
[19]:
# set up figure
fig, axes = plt.subplots(nrows=4,
ncols=2,
figsize=(12, 10),
sharex=True,
sharey=True)
# Set colorbar size
cbar_size = 0.5
# Set aspect ratios
for a in fig.axes:
a.set_aspect('equal')
# Set colorbar size
cbar_size = 0.7
stats = list(ts_stats.data_vars)
# Plot
for ax, stat_1, stat_2 in zip(axes, stats[0:4], stats[4:8]):
ts_stats[stat_1].plot(ax=ax[0],
cmap='cividis',
cbar_kwargs=dict(shrink=cbar_size, label=None))
ax[0].set_title(stat_1)
ts_stats[stat_2].plot(ax=ax[1],
cmap='plasma',
cbar_kwargs=dict(shrink=cbar_size, label=None))
ax[1].set_title(stat_2)
plt.tight_layout();
Next steps
When you’re done, if you wish to run this code for another region, return to the “Analysis parameters” cell, modify some values (e.g. time_range, or lat/lon) and rerun the analysis.
For advanced users, xr_phenology could be used for generating phenology feature layers in a machine learning classifier (see Machine Learning with ODC for example of running ML models with ODC data). xr_phenology can be passed inside of the custom_func parameter in the dea_tools.classification.collect_training_data() function, allowing phenological statistics to be computed during the collection of training data. An example
would look like this:
from dea_tools.temporal import xr_phenology
from dea_tools.classification import collect_training_data
def phenology_stats(da):
stats = xr_phenology(da)
return stats
training = collect_training_data(..., custom_func=phenology_stats)
Additional information
License: The code in this notebook is licensed under the Apache License, Version 2.0. Digital Earth Australia data is licensed under the Creative Commons by Attribution 4.0 license.
Contact: If you need assistance, please post a question on the Open Data Cube Slack channel or on the GIS Stack Exchange using the open-data-cube tag (you can view previously asked questions here). If you would like to report an issue with this notebook, you can file one on
GitHub.
Last modified: December 2023
Compatible datacube version:
[20]:
print(datacube.__version__)
1.8.11
Tags
Tags: sandbox compatible, NCI compatible, Sentinel-2, xr_phenology, dea_plotting, dea_bandindices, dea_datahandling, load_ard, calculate_indices, display_map, NDVI, EVI, time series, phenology, vegetation